Modulus of elasticity of concrete is the measurement of the stiffness of the concrete which is a good indicator of strength.
At a higher value of modulus of elasticity, the concrete can withstand higher stress and become brittle. In general, Concrete has an elastic modulus in a range of 30 to 50 GPa.
In recent years, design codes have specified a required minimum modulus of elasticity of concrete to be met. The objective is to limit the excessive deformation and sway in tall buildings.
Starin and strain are always associated. One causes another. Strain can also arise from other causes than applied stress.
For example, Creep and shrinkage strains.
The magnitude of shrinkage and creep strain is of the same order as elastic strain under the normal range of stresses. This is why all types of strain must be taken into account to calculate the deformation in a concrete member.
The expression for Modulus of Elasticity of Concrete
The expression for the modulus of elasticity of concrete, recommended by IS 456:2000 is
Ec = 5000 √fck
where fck is the characteristic strength of concrete.
Is concrete an elastic material?
Elasticity is the property of a material by which the material regains its original shape when the load is withdrawn.
Yes. Concrete is an elastic material to a certain extent i.e. at low stresses.
Concrete is a heterogeneous, multi-phase material, whose behaviour is influenced by the elastic properties and morphology of its component materials. So, the stress-strain curve does not exactly does not follow Hooke’s law.
The components of concrete i.e. cement paste and aggregates, when individually subjected to loading, they show almost linear stress-strain relation.
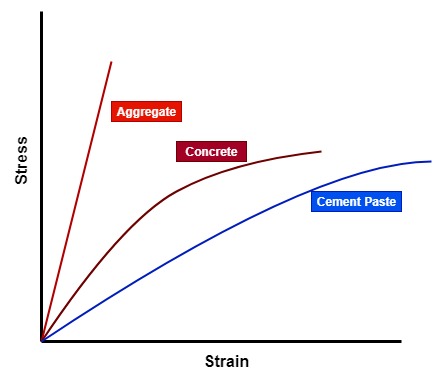
The cement paste has lower elastic modulus than the aggregate. The concrete behaviour is somewhere in the middle of both
Types of Modulus of Elasticity of Concrete
Static Modulus of elasticity
Static modulus of elasticity of concrete is defined as the slope of the stress-strain curve under uniaxial tension or compression loading.
When we test a concrete specimen in tension or compression, the following stress-strain relation is observed.
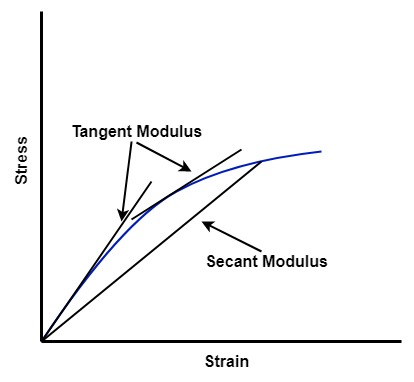
Young’s modulus of elasticity can be applied only to the linear portion of the stress-strain curve. When the curve for concrete is not straight any point, the modulus of elasticity is found out reference to a tangent drawn the curve at the origin. This is called the initial tangent modulus.
But it gives a satisfactory result at a low-stress value only. It is of no practical importance because it applies only to very small changes in load at which the tangent modulus is considered.
The strain in the specimen depends on the speed of loading. So it is difficult to differentiate between elastic and creep strains. For ease in understanding, any strain occurring during loading is called elastic and any subsequent increase in strain is called creep.
The modulus of elasticity of concrete which includes both strains is called Secant modulus or chord modulus. It is the common elastic modulus of concrete. It is given by the slope of the line drawn connecting a specified point on the curve to the origin of the curve.
The secant modulus is a static modulus because it is determined on a test specimen.
The secant modulus decreases with an increase in stress. So the stress at which secant modulus is determined must be mentioned.
Dynamic modulus of concrete
Dynamic modulus of elasticity of concrete represents the progressive changes in the state of a concrete specimen. The change can be observed by determining the fundamental resonant frequency of the specimen at appropriate stages of the investigation.


Thank you very much for the clarifications and explanations given. Please publish how the elastic modulus is calculated in the laboratorty experient.
very value able.. thank you